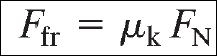FORCES AND FRICTION
Unit
Overview
This
unit will focus on the effects of friction, both one dimensionally and in two dimensions.
You will see how friction opposes the motion of an object to slow it down, or
make it impossible to move. We will also explore how other forces like a push
or pull, gravity and friction all work together in Newton’s second law of
motion as learned about in units 6 and 7.
Friction
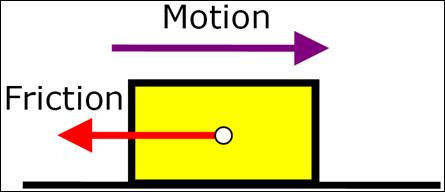
Friction is a force that acts in a direction
parallel to the area of contact, and opposes the motion or the tendency to
move. There are two kinds of friction, static and kinetic. Static Friction is the
friction force that opposes motion and is equal to or greater than the force
trying to move the object. So the object trying to move cannot, and it is at
rest. Eventually the object will
move when more force is added to the object, which tells us that static
friction can only be so great. Kinetic
Friction is the frictional force
exerted on one surface by the other when the surfaces are in relative
motion. Even if an object is able to
move, there will still be friction between the object’s surface and whatever
the object is moving on top of. There
are 6 simple principles about friction, which will be helpful to consider when
dealing with problems to determine if friction will be a factor, and when it
will not.
|
|
|
1.
Friction acts parallel to the surfaces in contact and opposite the motion of
the object.
|
|
2.
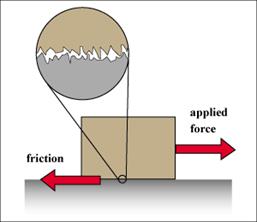
Friction depends on the nature of the materials in contact and the smoothness
of their surfaces. Even
materials that appear to be smooth have microscopic irregularities on its
surface causing friction.
|
|
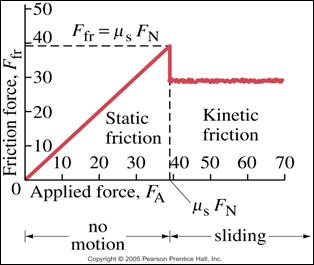
3. Starting friction is greater than
sliding/rolling friction. The static frictional force increases as the
applied force increases, until it reaches its maximum. Then the object starts
to move, and the kinetic frictional force takes over. Therefore static
friction is always greater than kinetic Friction
|
|
4.
Sliding friction is practically independent of speed. Once
an object starts moving the only thing that really matters is the surface of
the materials moving past one another |
|
5.
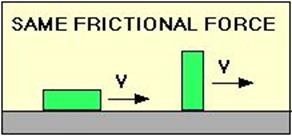
Friction is practically independent of the area of contact. Surface
area does not make something have more or less friction. |
|
|
|
6.
Friction is directly proportional to the force pressing the two surfaces
together. In
other words; the heavier the object is, the more friction there will be
opposing its motion. (i.e., it’s harder to
push a truck than it is to push a sports car) |
|
|
Solving
for Friction in One Dimension
In order to
solve for friction we must first look at whether the object is at rest or if it
is moving. If it is at rest we are dealing with static friction. If it is
moving, it is kinetic. Next we will consider what materials are in motion and
what surface it is moving on top of.
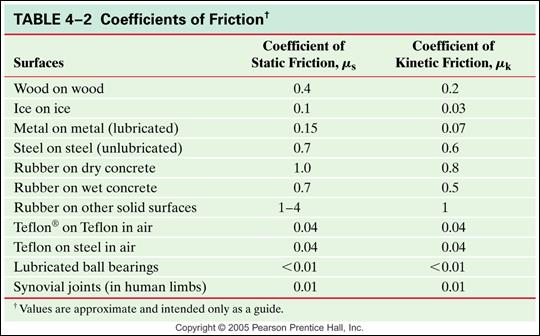
This will determine the coefficient
of friction value for the problem. As the surface changes, the coefficient
of friction changes. Below is a table that shows some common surfaces coming
into contact with one another and then what the coefficient of static and
kinetic friction would be.
Mass of the
object that is moving is another factor in determining the amount of friction
acting on the object. The heavier the object, the more friction there will be.
The final factor to consider is gravity. Gravity is acting on an object to pull
it down against the surface.
By looking at
those factors concerning friction, it yields the equation:
|
|
|
Where Ffr is the force of friction, |
![]() Kinetic and Static Friction (02:37)
Kinetic and Static Friction (02:37)
Solving problem hints:
·
When
velocity is constant or zero, the force of friction is equal to the applied
force.
·
Always
sum your forces on one side before solving for anything else
·
Draw a
force diagram for every problem
·
Don’t
forget Newton’s second law – F = ma as well as your kinematics equations from
Unit 2
|
Examples: |
|
1. A box with a mass of 20 kg is
resting on a table. The coefficient of static friction is .4. What is the
force of friction acting on the box? |
|
|
|
|
|
2. You are pushing your little brother
at a constant speed on a sled horizontally with a force of 40N, he has a mass
of 30 kg, what is coefficient of kinetic friction? |
|
|
|
|
|
3. A force of 55 N accelerates a 6 kg
block at 3 m/s2 across a horizontal surface. How large is the
frictional force and what is the coefficient of friction? |
|
|
|
When solving for Ffr we will use the
equation F = ma. In order to do this you must use the sum of the forces for F
on the left side of the equation. In this problem we have an applied force
and a force of friction. Because friction always acts in a direction opposite
of motion we will subtract friction from the applied force to give us one F. |
|
|
|
4. You are ice skating and gliding with
an initial speed of 7m/s and glide to a stop. How far will you go, given the
coefficient of friction is .08? |
|
|
|
Because the problem says that you are
gliding with a velocity of 7 indicates that at this moment there are no
applied forces acting on you to make you move. So the only force acting
against your motion is friction. |
|
|
|
|
Friction
in Two Dimensions
The
above scenarios all depicted a situation where an object was moving along a
flat horizontal surface, but what happens when the object is moving downhill or
on a slope? In these types of situations gravity plays a huge role in
accelerating the object downhill at an angle relative to a horizontal plane. In
this case we need to come up with a coordinate system. We will say the slope of
this hill or incline is the x axis and the y axis is perpendicular to the
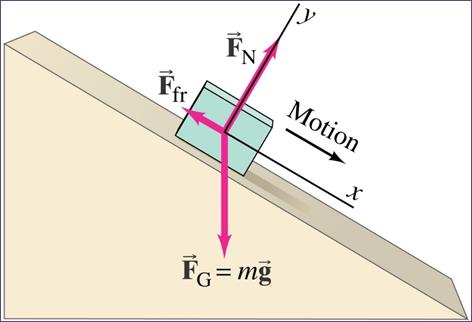
incline or hill. By looking at the picture below, you can see the direction of
forces acting on the block: the normal force is perpendicular to the incline.
An
object sliding down an incline has three forces acting on it: the normal force,
gravity, and the frictional force.
•
The normal force is
always perpendicular to the surface.
•
The friction force is
parallel to it, opposing gravity in the x direction
•
The gravitational or
weight force points straight down.
•
There may also be an
applied force acting on the object if something is pushing or pulling it
Now
that an object is moving “downhill” there will be a horizontal gravity
component and a vertical gravity component. The natural acceleration of the
object down an incline is due to gravity in the x direction.
Weight components equations:
Fgx
(gravity in the x direction) = mg sin theta
Fgy
(gravity in the y direction) = Fn = mg cosine theta – According to Newton’s
second law (F=ma) they are equal to one another because acceleration is zero in
the y direction
Hints:
The
angle of the incline given is the same angle between the normal force and the
weight force. When you find Fn and Fgx this is the similar triangle that you
will use to break it up into its components. Which is why in most cases we will
use the sin trig function to find Fgx and the cosine trig function to find Fn.
Acceleration
in the Y direction is always zero.
|
Examples:
|
|
1. A 5 kg block slides down a 26 degree
inclined plane with a constant acceleration of .25 m/s 2. The block starts
from rest at the top. |
|
A.
What is the Force of Friction? |
|
|
|
B. What is the Coefficient of Friction |
|
|
|
2.
A skier with a mass of 65 Kg is going
down a slope that has an incline of 30 degrees because her friend pushed her
with a force of 5.3 Newton’s. Assuming the coefficient of kinetic friction is
.10, what is her acceleration? |
|
|
|
|
|
3. A skier with a mass of 50 kg starts
from rest and slides down an incline with an acceleration of 3 m/s2. If the
force of friction acting against the skier is 22 N, what is the incline of
the hill in degrees? |
|
|
Looking
Ahead to Unit 9
In unit 9 you will explore friction in one dimension by completing a laboratory exercise. You will be able to manipulate the mass of an object, the materials of the surfaces and the initial velocity of the object.

Below are additional educational resources and activities for this unit.